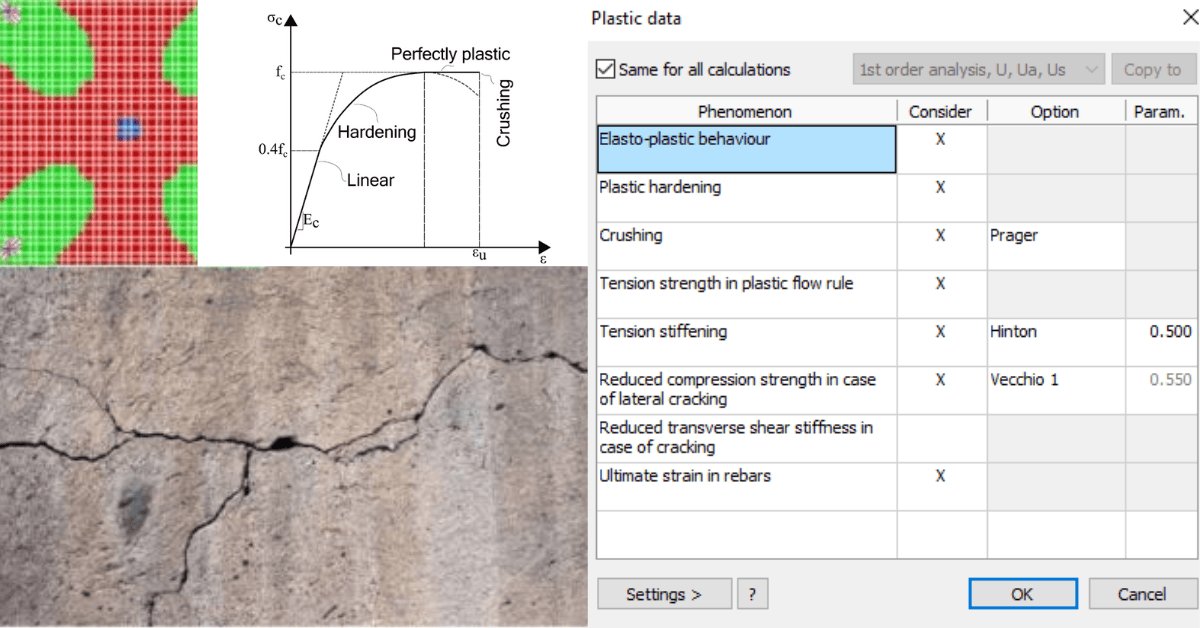
Reinforced Concrete Design
The Reinforced Concrete Design Software, FEM-Design, is a powerful design tool to help you design both Reinforced Concrete (RC) and Precast Concrete structures.
The reinforced concrete design is complete, simple and fast regardless of whether you have examined objects in a complete 3D modelling environment, or element by element in a 2D view.
Reinforced Concrete Bar Design
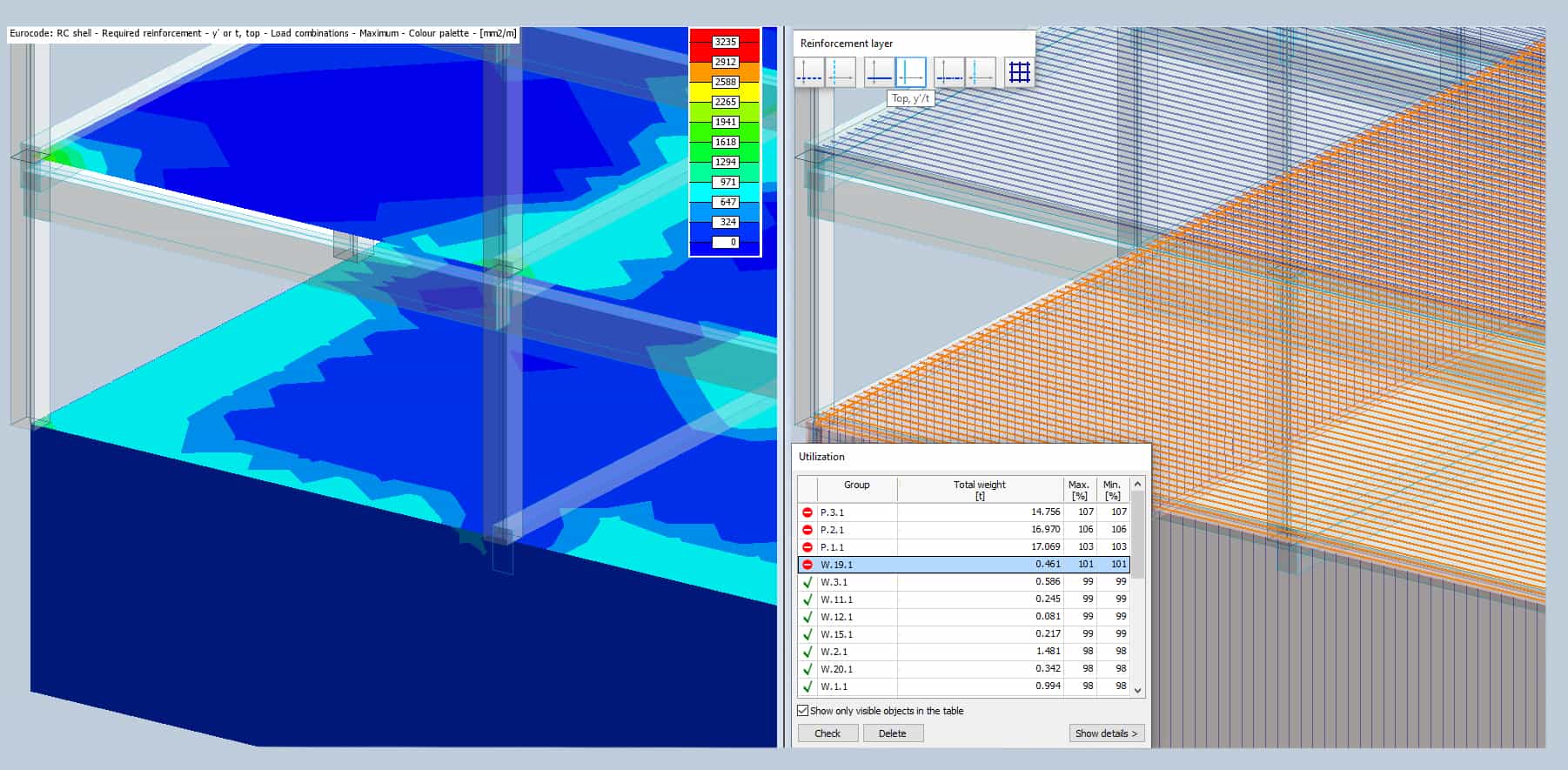
Reinforced Concrete Shell Design
Different kinds of detailed design results of RC shells, such as required and missing reinforcement, shear capacity, shell buckling and crack width are providing feedback about the design capacity. These unique results are supplemented with Utilisation results, which aim to consider all the available results for RC shells. They are available for each load combination, maximum of load combinations and maximum of load groups. We can also set where to consider compressed reinforcement or non-shear regions.
Reinforced Concrete Cracked Section Analysis
Cracked-section analysis of RC shells and bars calculates displacement based on the cracked state and designed reinforcement of objects and an iteration mechanism. Considering elements, crack effect is a non-linear calculation, loading the structure in load steps and modifying the stiffness in every step to generate more and more cracks.
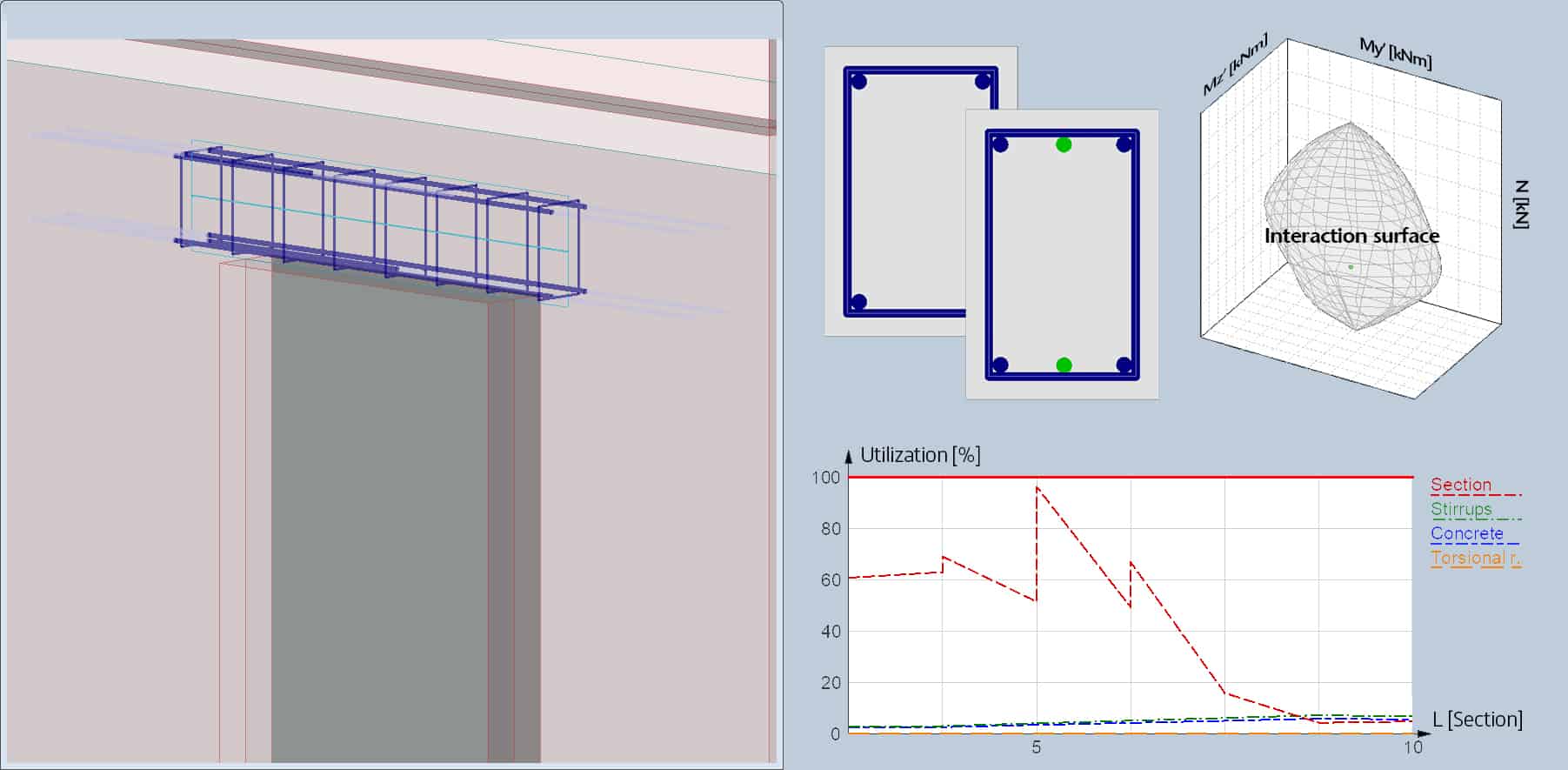
Concealed Bar Design
Concealed bar is a new RC design object that allows for designing certain parts of a shell as a bar. For example, a wall region over a door opening can be considered as a concealed beam. Manual and automatic design process for concealed bars is the same as for individual RC bars. Listed tables and displayed results are also similar, but concealed bar’s internal forces – derived from the shell’s internal forces – are also listed and displayed.
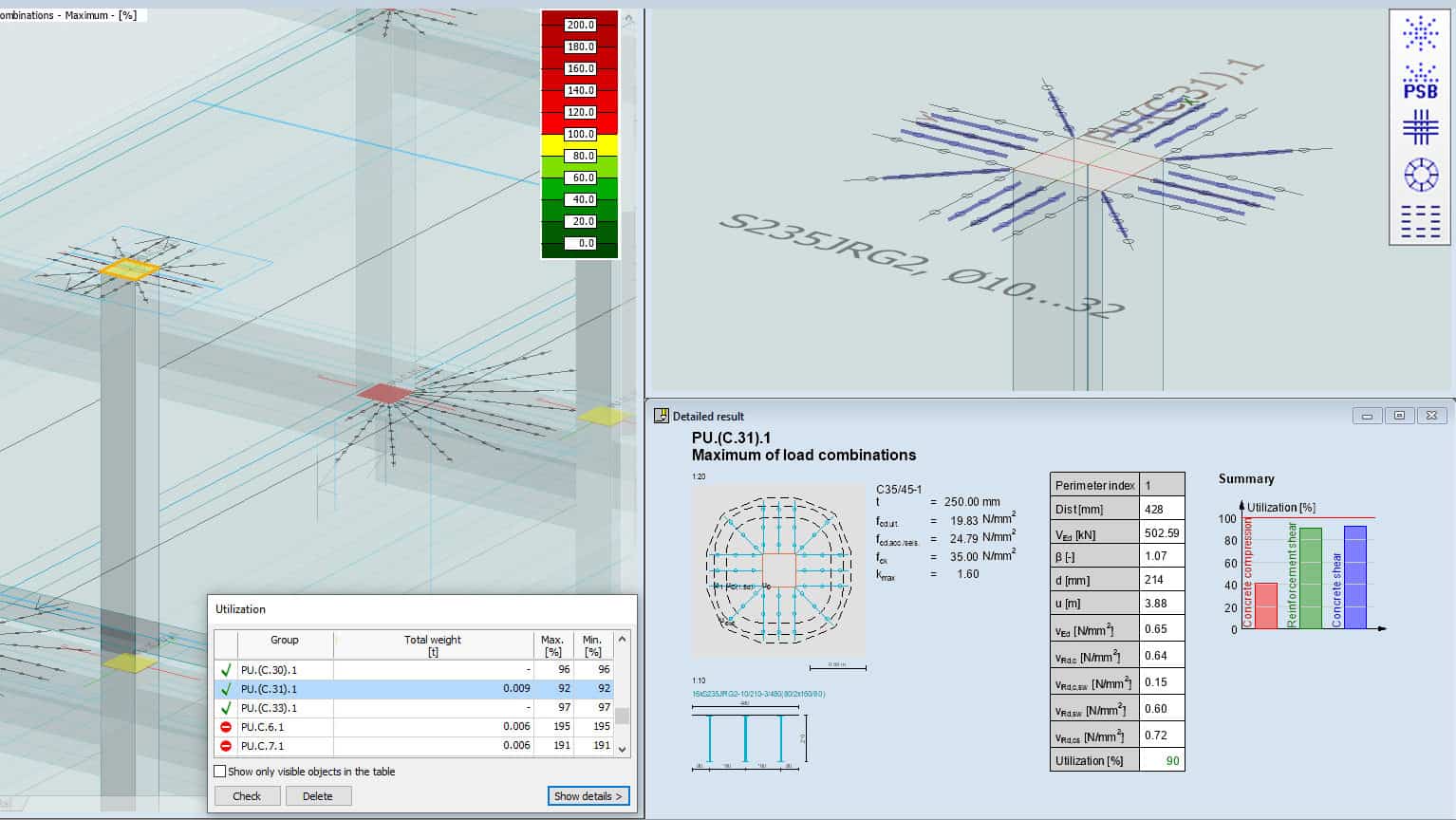
Punching Reinforcement Design
Punching check and design can be done according to Eurocode 2. The punching regions are automatically defined by the program at the plate–column intersections and wall ends, or you can define them manually.
Precast Concrete Design
The FEM-Design software also has all the tools you need to analyse and design precast concrete structures.
The key to good analysis results in precast concrete lies in the connection conditions and types. Defining both elastic and plastic connections is an easy task in FEM-Design. All connection and support components can be set to “infinite” rigid, semi-rigid or free.
Benefits of using the FEM-Design Concrete Design Module
Detailed Design Checks to Eurocode 2
Pick a concrete member of a complex mixed structure and check or optimise its geometry and reinforcement according to Eurocode 2 and National Annexes.
Limitless Analysis and Design Features
Let’s highlight some enhanced features: support environment as non-linear soil, non-linear elastic calculation, plastic analysis, cracked-section analysis, second-order analysis, stability and dynamic check, consideration of imperfection, earthquake and fire effect.
Detailed Documentation Reporting
Numerous documentation possibilities are available for reinforced concrete design and check. Graphs, images, equations, tables and texts can build complete documentation in unique styles and for printing it as PDF, editable Word doc. format, Mathcad input or hard copy.
Versatile Dimensioning of Columns & Beams
FEM-Design designs and dimensions columns and beams either with an easy-to-use reinforcement editor or fully automatically, considering anchoring and second-order effects and other essential inspections in accordance with the standard.
Why wait? Apply below to download a trial license of FEM-Design and get started on your journey today!
Calculations performed according to:
Euro Code- Belgian National Annex
- British National Annex
- Danish National Annex
- Dutch National Annex
- Estonian National Annex
- Finnish National Annex
- German National Annex
Euro Code
Belgian National Annex
British National Annex
Danish National Annex
Dutch National Annex
Estonian National Annex
Finnish National Annex
German National Annex- Hungarian National Annex
- Latvian National Annex
- Norwegian National Annex
- Polish National Annex
- Romanian National Annex
- Spanish National Annex
- Swedish National Annex
- Turkish Seismic Code
Hungarian National Annex
Latvian National Annex
Norwegian National Annex
Polish National Annex
Romanian National Annex
Spanish National Annex
Swedish National Annex
Turkish Seismic CodeLanguages supported:
- English
- Finnish
- French
- Dutch
- Hungarian
- Polish
English
FrenchFEM-Design Wiki
Full details on the RC Design and the theory can be found on the FEM-Design Wiki by clicking here.
FEM-Design Blog
FEM-Design 23 – Greater Efficiency: Save Time, Save Materials
FEM-Design 23 is released and introduces a brand-new 3D Bridge module, a new plastic analysis method, a renewed documentation module, and several significant improvements [...]
Plastic shell modelling in FEM-Design 23 for steel and reinforced concrete
Introduction into plastic shell modelling with FEM-Design FEM-Design 23 comes with a new module for non-linear calculations. It combines the existing features for plastic [...]
Free structural analysis software for students 2024
You’re an ambitious student eager to dive into structural engineering. We’re here to help you in your journey as your partner in structural analysis [...]
Bio: Mikael van de Leur is the Head of Sales at StruSoft, for the Structural Business Unit. He has been with StruSoft since 1995 and has ...show more many years hands-on experience in all our different structural software, as well as in customer relationships and sales. Mikael coordinates the Structural Sales Team and Customer experience for new customers in StruSoft’s International markets. show less
Bio: Anders Nilsen is Sales Manager at StruSoft and based in Denmark. He joined StruSoft in 2019 and has a background as a civil engineer with ...show more lots of practical experience in all our structural software. In addition to sales, Anders also manages our sales and customers experience teams in Denmark and Poland. show less
Bio: Isak Björhag works as Business Development Manager for new markets. Isak has many years of experience both with hands on practical engineering and working with our ...show more customers helping them to succeed with our structural engineering software. This can be achieved through specific training, presentations or hands on demonstrations for specific cases. Please feel free to contact Isak if you are interested in a demo or want to expand your knowledge in our structural software. show less
Bio: Johanna Riad is an Automated Workflow Specialist for StruSoft, based in our Gothenburg office. Johanna works with building customised workflows for our customers with the ...show more help of application programming interfaces (API's). Johanna can support you with consultancy, training courses and developing custom automated workflows for your structural design challenges. This might be anything from simple Excel scripts to more advanced processes, where several different software programs can be connected, to leverage the power of parametric modelling and computational design. Please feel free to get in touch directly with Johanna for any API related enquiries or support. show less
Bio: Joni has helped and trained hundreds of engineers in structural analysis in Finland. He works in both civil and mechanical engineering fields with structural analysis. ...show more Joni has over 15 year of experience in structural design of many types and sizes of steel, concrete and timber structures. Joni is the Product Owner of our JIGI software and Country Manager for Finland. Please free to contact Joni if you need any help to solve your structural analysis problems. show less
Bio: Mohsen Ghaemi is the Regional Manager for StruSoft in our Structural Business Unit. He has a PhD in Structural Civil Engineering (Topology optimisation). Mohsen has ...show more been with StruSoft since 2002 and has more than 20 years of experience with the FEM-Design software and its development, as well as in customer relationships and sales. Please feel free to get in touch with Mohsen directly. show less
Bio: Edris Mohammadi Nikzad is a Costumer Success Manager at StruSoft, based in our Stockholm’s office. He joined StruSoft in 2019 and has many years of ...show more experience on practical engineering and working with FEM-Design and WIN-Statik. Edris works closely with our customers in Sweden to help them to succeed with our structural engineering software. If you are interested in a demo of our calculation programs for a specific purpose, or if you have a special request for any training, please feel free to contact Edris. show less
Bio: Marek Krawczyk is the Country Manager for Poland at StruSoft. As a structural engineer, he has more than ten years of international experience, working on ...show more various projects in Europe, the UK, the USA and Asia. He joined StruSoft in 2022 to strengthen our presence in Poland and support the StruSoft software Users in the local market. show less
Bio: Suleyman Sayed, also known as Sulo, is the branch manager for Matrix's structural engineering software products, StruSoft's sister company in The Netherlands. Currently, he primarily ...show more focuses on expanding market share and devising strategies to better position FEM-Design in the Netherlands, the Dutch Antilles, and Suriname. With his extensive background in structural engineering, deep market knowledge, and experience in various industries such as petrochemicals and civil construction, Sulo is well-equipped to offer customized solutions that perfectly meet the needs of his clients. show less
Bio: Markus Mitikka is a customer coach for StruSoft in Finland. He has previous experience of FEM calculations and structural designs working for engineering office. He ...show more was a big fan of StruSoft software before joining StruSoft in beginning of 2022. Markus can help you to become more efficient with all our structural software. Please feel free to get in touch. show less
Bio: Casper Hougaard is a Customer Coach for StruSoft's Structural Team based in Denmark. He joined StruSoft in 2022 and has a background in civil engineering ...show more with lots of practical experience using FEM-Design. Casper would be happy to help any Danish FEM-Design Users with general guidance, project specific guidance and training. show less
Bio: Ciprian Tibea is the Head of Sales for Baltics & Romania and has been with StruSoft since 2018. Ciprian has a PhD in Civil Engineering ...show more (Ultra High Performance Concrete Subjected to Shear Action) and a Masters Degree in Entrepreneurship and Business Administration. Prior to StruSoft, Ciprian was working as a research engineer for Consolis for 6 years and for 1 year with a local company in Romania working on structural design projects with advanced Finite Element Software (Diana and Atena). Ciprian is your main Structural Sales contact for markets outside Europe, the Baltics and Romania. Please feel free to get in touch. show less
Bio: Suhas is the Managing Director of StruEngineers India, a Design & Detailing Service company 100% owned by StruSoft. Suhas has a BSc in Civil Engineering ...show more and has been providing design support services to the Precast Industry, worldwide, over the last 20 years. Suhas was one of the original founders of StruEngineers which was established 10 years ago and previously worked for Neilsoft in Pune. StruEngineers provides local support in India for all StruSoft software and Suhas is a specialist with IMPACT AutoCAD. If you are based in India and looking for more information or support please feel free to get in touch directly with Suhas. show less